User:Jorend/Deterministic hash tables

Abstract

A deterministic hash table proposed by Tyler Close was implemented in C++ and its performance was compared to two hash table implementations using open addressing. Speed and memory usage were measured.

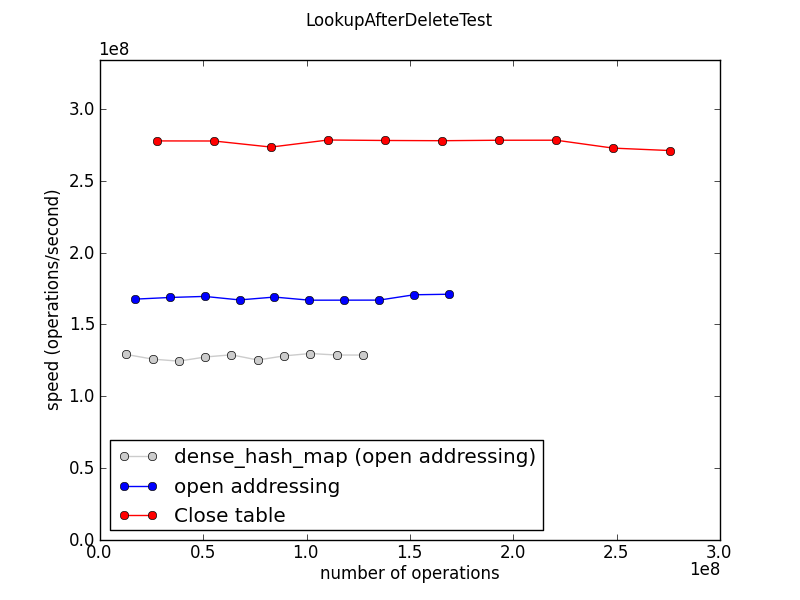
Speed. The Close table implementation was very fast, faster than the open addressing implementations. (It is unclear why; theory suggests it "should" be slower, and measurement confirms that the Close table is doing more memory accesses and more branches. More investigation is needed!)

Memory. The Close table implementation allocates 29% more memory on average than the leanest open addressing implementation on 32-bit systems, 29% more on 64-bit systems.

Background

Most hash table APIs (including C++'s unordered_map, Java's java.util.HashMap, Python's dict, Ruby's Hash, and many others) allow users to iterate over all the entries in the hash table in an arbitrary order. This exposes the user to an aspect of the library's behavior (the iteration order) that is unspecified and indeed intentionally arbitrary.

Map and Set data structures are proposed for a future version of the ECMAScript programming language. The standard committee would like to specify deterministic behavior if possible. There are several reasons for this:

• There is evidence that some programmers find arbitrary iteration order surprising or confusing at first. [1][2][3][4][5][6]
• Property enumeration order is unspecified in ECMAScript, yet all the major implementations have been forced to converge on insertion order, for compatibility with the Web as it is. There is, therefore, some concern that if TC39 does not specify a deterministic iteration order, “the web will just go and specify it for us”.[7]
• Hash table iteration order can expose some bits of object hash codes. This imposes some astonishing security concerns on the hashing function implementer. For example, an object's address must not be recoverable from the exposed bits of its hash code. (Revealing object addresses to untrusted ECMAScript code, while not exploitable by itself, would be a bad security bug on the Web.)

Can a data structure retain the performance of traditional, arbitrary-order hash tables while also storing the order in which entries were added, so that iteration order is deterministic?

Tyler Close has developed a nondeterministic hash table that is structured like this (pseudocode):

struct Entry {
    Key key;
    Value value;
    Entry *chain;
}

class CloseTable {
    Entry*[] hashTable;  // array of pointers into the data table
    Entry[] dataTable;
}

Lookups and inserts proceed much like a bucket-and-chain hash table, but instead of each entry being allocated separately from the heap, they are stored in the dataTable in insertion order.

Removing an entry simply replaces its key with some sentinel while leaving the chain intact.

Method

The code I used to make these pictures is available at: https://github.com/jorendorff/dht

(These particular graphs show data collected on a MacBook Pro, using g++-apple-4.2 and a 64-bit build. The results from running the test on a 32-bit Windows build were qualitatively similar.)

The project contains two complete hash map implementations: OpenTable and CloseTable. A third implementation, DenseTable, is a thin wrapper around the dense_hash_map type from Sparsehash. The three classes have the same API and were all benchmarked using the same templates (in hashbench.cpp).

Hash table implementation design notes:

• The API was designed to match the proposal for ECMAScript Map objects as of February 2012.

• The Key and Value types are uint64_t because ECMAScript values are 64 bits in the implementation I'm most familiar with.

• OpenTable and CloseTable are meant to be as fast and as memory-efficient as possible. Pretty much everything that can be omitted was omitted. For example, the hashing function is trivial: hash(key) = key, and neither OpenTable nor CloseTable further munges the hashcode before using it as a table index. Rationale: Making each implementation as fast as possible should highlight any performance difference between OpenTable and CloseTable, which is the purpose of the exercise. Using a more sophisticated hashing function would slow down both implementations, reducing the observed difference between the two techniques.

• DenseTable is provided as a baseline. (It's nice to have some realistic numbers in the graphs too.)

• dense_hash_map and OpenTable both implement straightforward hash tables with open addressing. The main difference between the two is one of tuning. dense_hash_map has a maximum load factor of 0.5. OpenTable has a maximum load factor of 0.75, which causes it to use about half as much memory most of the time.

• The purpose of the typedefs KeyArg and ValueArg is to make it possible to switch the API from pass-by-value to pass-by-reference by editing just a couple of lines of code. (I tried this. Pass-by-reference is no faster on 64-bit machines.)

• CloseTable attempts to allocate chunks of memory with sizes that are near powers of 2. This is to avoid wasting space when used with size-class-based malloc implementations.

• A Close table can trade some speed for compactness, but it seems to be a bad bargain:
  • The load factor is adjustable. (The hash table size must remain at a power of two, but the data vector can have non-power-of-2 sizes.) However, increasing the load factor directly affects LookupMiss speed.
  • An implementation could grow the data array by less than doubling it each time. I tried this. Insert speed suffered; lookup speed was unaffected; but the modified CloseTable still used more memory than OpenTable.

• dense_hash_map never shrinks the table unless you explicitly ask it to. DenseTable::remove() periodically shrinks, because otherwise, the performance on LookupAfterDeleteTest is pathologically bad.

Benchmark design notes:

• There would be more tests but it takes a long time to write them. Feel free to send me pull requests.

• The program runs each benchmark many different times in order to produce enough numbers that noise is visually obvious in the resulting graph. (Most of the speed graphs are nice and smooth.)

Results

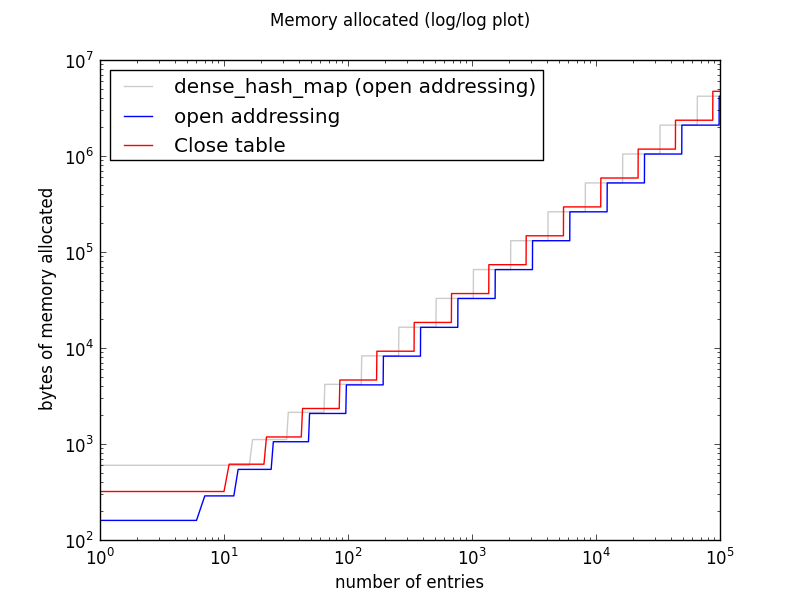
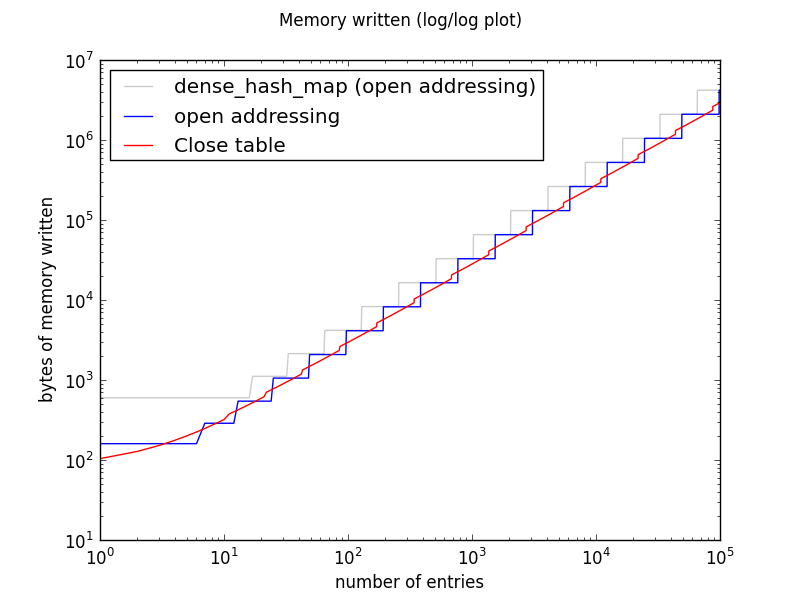
Memory usage

All three implementations double the size of the table whenever it gets too full. On a log-log plot, this shows as stair-steps of a constant height. The slope of each staircase is 1, indicating linear growth.

CloseTable is much more memory-efficient than DenseTable, because the latter is tuned for fast lookups at all costs.

DenseTable and OpenTable must initialize the entire table each time they resize. CloseTable also allocates large chunks of memory, but like a vector, it does not need to write to that memory until there is data that needs to be stored there.

This means that for a huge Map with no delete operations, a Close table could use more virtual memory but less physical memory than its open addressing counterparts. This will not be the only use case that stresses memory usage, though. Applications may also create many small tables and may delete entries from large tables.

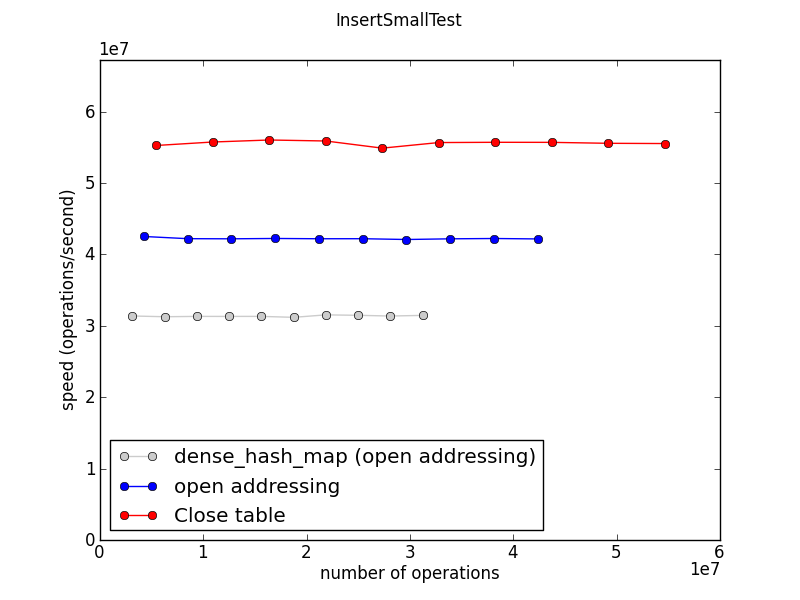
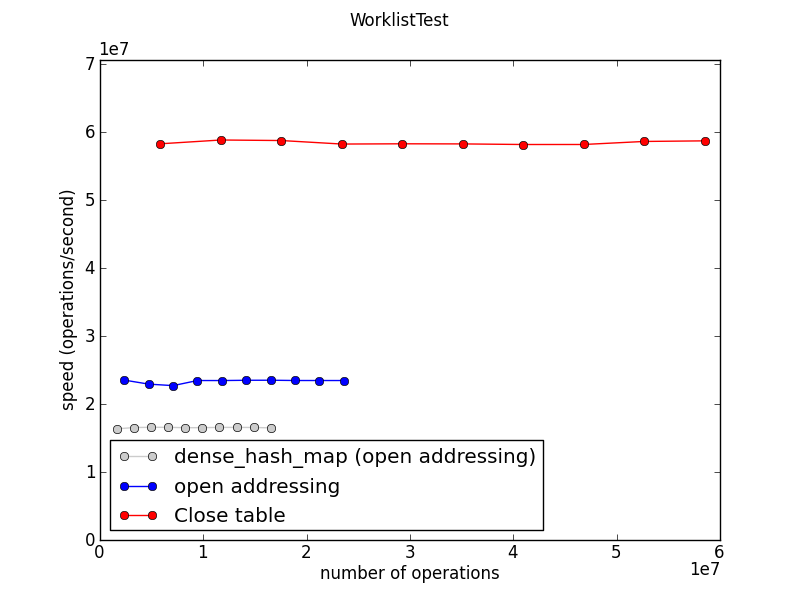
Insertion speed

This measures the time required to fill a table to about 100 entries, repeatedly. (The “1e7” on the axes indicates that the numbers are in tens of millions: the Close table is doing about 60 million inserts per second on this machine.)

This graph and the following ones show speed, so higher is better.

Ideally all these graphs would show three straight horizontal lines, indicating that all three implementations scale beautifully to large work loads. And indeed this seems to be the case, mostly.

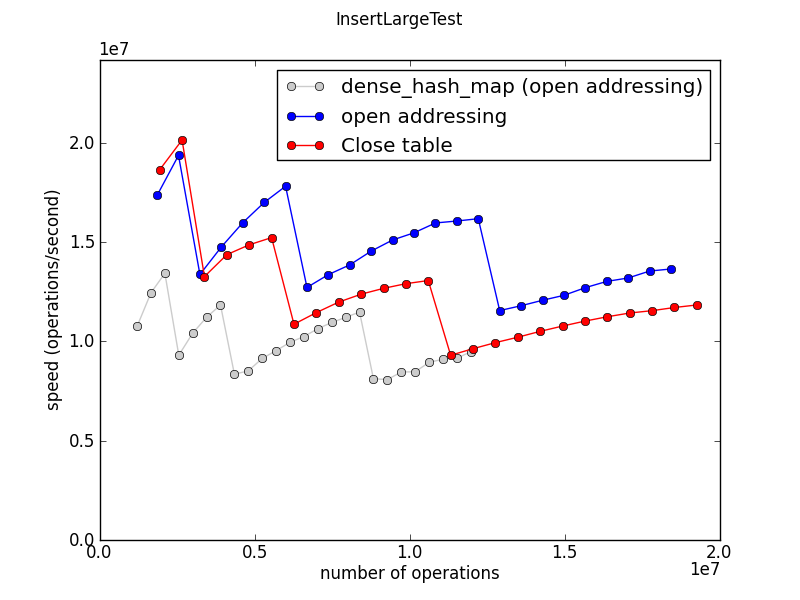
This test measures the time required to fill a single gigantic table.

The jagged shape of this graph is robust. It reflects the fact that the table doubles in size as it grows, and rehashing is a significant part of the expense of populating a huge table.

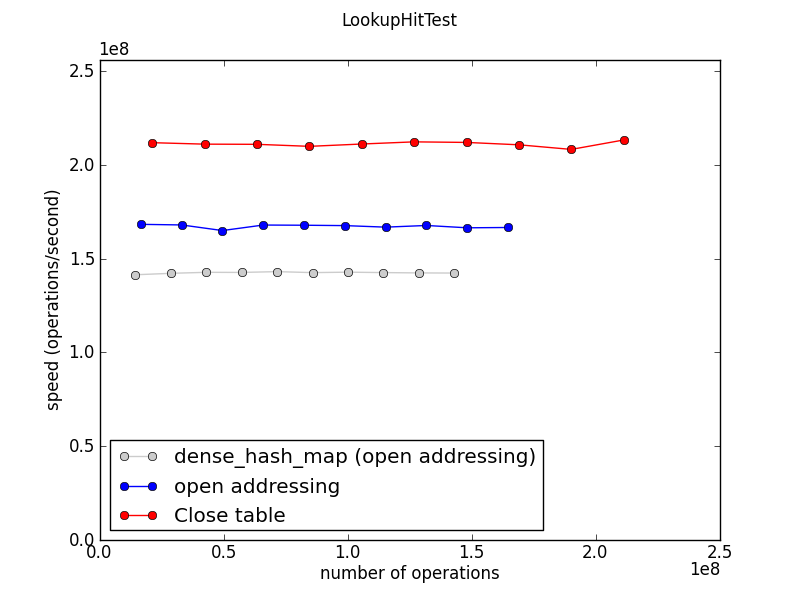
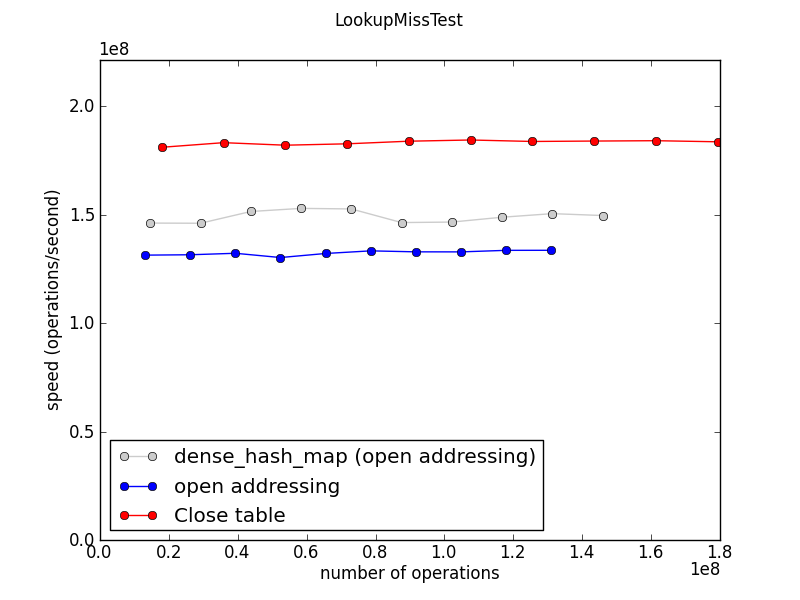
Lookup speed

In an OpenTable, lookups that miss are slower than lookups that hit when there is at least one collision. This is because we keep probing the hash table until we find an empty entry.

DenseTable is only slightly slower for misses, perhaps because more lookups have zero collisions. (?)

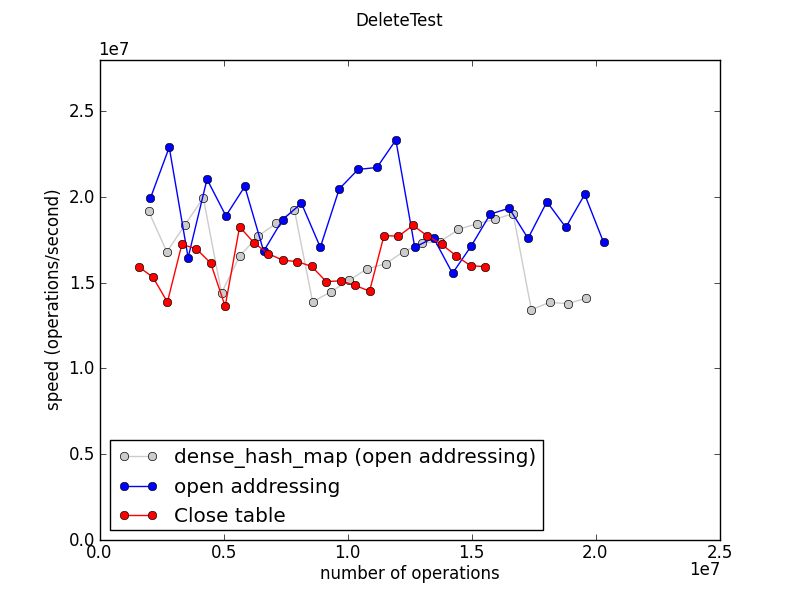
Deletion speed

This test creates a table with 700 entries, then measures the speed of alternately adding an entry and deleting the oldest remaining entry from the table. Entries are therefore removed in FIFO order. Each “operation” here includes both an insert and a delete.

This test measures the speed of deleting all entries from a very large table.

The numbers for dense_hash_map are jagged because DenseMap shrinks the table at certain threshold sizes as entries are deleted, and shrinking the table is expensive.

The apparent randomness of the OpenTable and CloseTable numbers is unexplained.

This test measures the performance of lookups, mostly misses, in a table that was filled to size 50000, then reduced to size 195 by deleting most of the entries.