Identity/CryptoIdeas/01-PBKDF-scrypt

Key-Wrapping Techniques

• Brian Warner, 05-Apr-2012

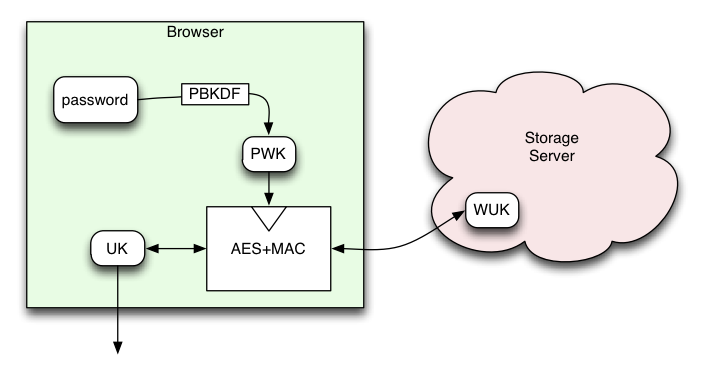
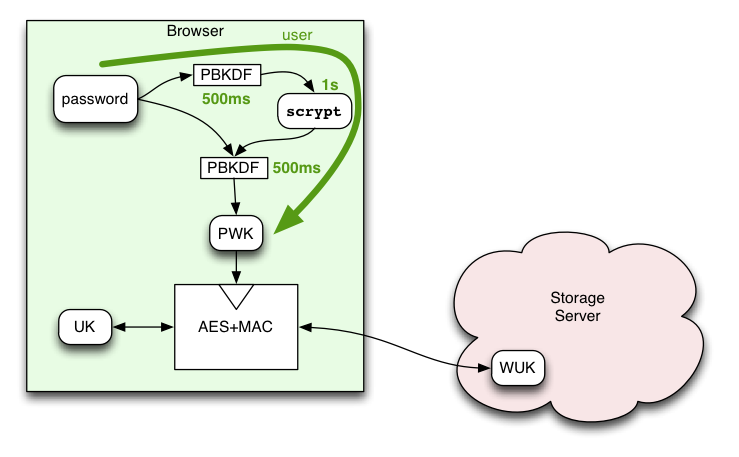
The basic key-wrapping proposal in BrowserID Key Wrapping describes an layered arrangement of encrypted keys that allow arbitrary sites (e.g. Firefox Sync) to obtain full-strength per-domain encryption keys, which the user can regenerate any time they like using a password and information stored on the BrowserID storage server. From the point-of-view of such services, these keys really are full-strength: 256 bits of pure entropy. The system looks basically like this:

Attacks

Since this model allows the user to get at their data using nothing but a password and the data stored on the Primary, there must be places in the system for which the keys are less than full strength. The most vulnerable point is the server which holds the wrapped user key ("WUK"). In general, attackers can be categorized into a few different groups:

network eavesdroppers 

since all connections are assumed to run over SSL, which does a great job of protecting against passive eavesdroppers, these attackers have nothing to work with

man-in-the-middle 

SSL does a less-great job of protecting against active attackers. There are too many CAs, users do not have enough information to identify the "right" site, and the security indicators are too fragile for users to reliably notice.

Storage Server and Friends 

the server holds the WUK, as well as other verification data used to decide whether to honor requests to update the WUK later, both of which can be used to attack the user's password and thus the Password-Wrapping-Key (PWK), which then combines with the WUK to get the ultimate goal: the User Key (UK). This category of attacker includes anyone who can get access to the WUK: admins of the server, anyone who successfully breaks into the server or gets a copy of a backup disk, and any party who can coerce/subpoena the admins into revealing a WUK.

In general, attacks must start by stealing/possessing an "oracle" value (like the MAC portion of the WUK) which allows them to test whether a given password is correct or not. Then the attacker generates guesses for the user's password (which is the most predictable value in the system) and runs through same protocol as the user would, until they get to a value which can be tested against their oracle. They must do this a lot, since there are lots of possible passwords, so they're interested in minimizing the cost of each attempt.

Remember: the cost figures described below are talking about an attacker who has already surmounted the difficult hurdle of breaking into a professionally-managed highly secure server, either by force, coersion, or subpoena. These attacks are not available to a passive eavesdropper or a network-side man-in-the-middle: those folks don't have any feasible attack.

PBKDF User/Attacker Costs

We can evaluate various techniques according to how much they cost the user (in units of time spent waiting for a login) versus how much they cost the attacker (in units of dollars spent finding a password).

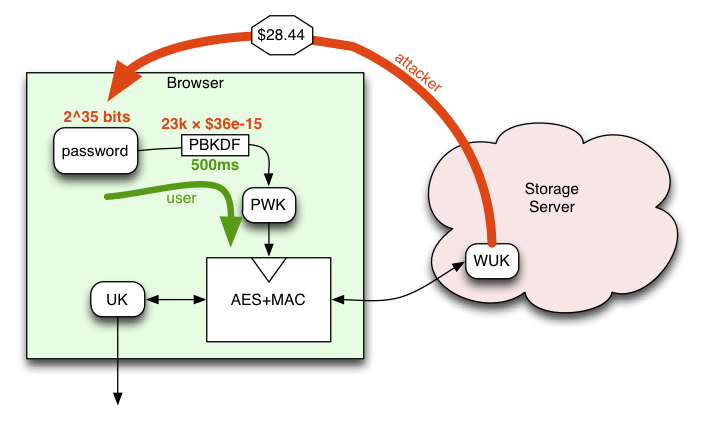
To start with, it's reasonable to hope that the user's password contains about 35 bits of entropy (when expressed as groups of purely-random base32 characters, this looks like "rf-o5m-t6"). Some users may use better generation techniques, some worse. The attacker's costs scale directly with the space of passwords that must be searched: a user who can make passwords with 40 bits of entropy will increase the attacker's costs by 32x over the baseline explored here. Someone who uses 6-digit PINs (20 bits) will lower the attacker's costs by 32768x.

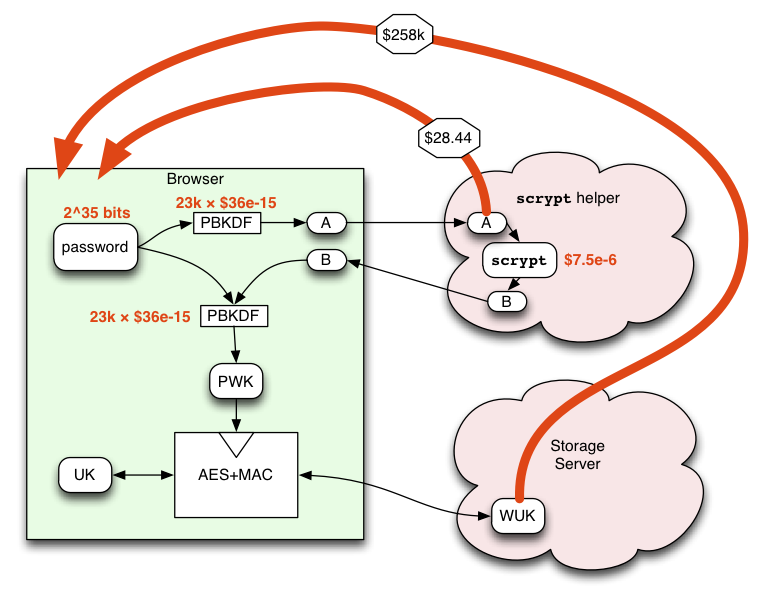
PBKDF is basically multiple rounds of SHA256 hashing, designed to increase the cost of a brute-force attack. My 2010 MacBookPro takes about 22us to do each PBKDF iteration in Javascript (using the SJCL library), and we can probably get away with a 500ms delay in the login process. This gives us about 23k iterations of PBKDF, and a user cost of about 500ms.

Unfortunately, the attackers aren't limited to Javascript or the CPU in my laptop. A real attacker will use a highly-optimized GPU, which can do roughly one billion SHA256 hashes per second (1ns per iteration). We can use the Bitcoin network statistics and exchange rates to estimate the cost (including both the GPUs and the electricity) of doing a SHA256 hash using state-of-the-art technology. This works out to about $36*10^-15 (femtodollars) per hash, e.g. one USD will buy you about 28*10¹² = 28 trillion hashes. (as of 05-Apr-2012, where DF=1.626M, yield=50BTC/block, 1 block/10min, hashrate=11.37Thps, and a mtgox price of $4.91/BTC).

This results in a brute-force cost of about $28.44 per key, for an attacker in the "Storage Server and Friends" category. Note that this cost is per-user: by using the user's email address as a salt, the attacker is forced to attack each key separately (without the salt, they could attack all user accounts at the same time, and amortize the costs).

Anyone who can view the WUK in transit (perhaps man-in-the-middle attackers) can perform the same attack. Below we'll talk about using SRP to prevent some forms of this attack.

scrypt() Helper

scrypt (http://www.tarsnap.com/scrypt.html) is a memory-hard key-derivation function, designed specifically to deny the GPU speed advantage by using significant memory (and memory bandwidth). GPUs have many small fast processors, but do not have large amounts of generally-addressable RAM. By using scrypt as a busy-work function, attackers have to use computers that are roughly similar to the user's computer, increasing the attacker's costs.

Unfortunately it is not yet clear that scrypt can be computed efficiently in Javascript. The algorithm, of course, can be computed by any Turing-complete language. However, the per-object memory overhead and additional operations required to perform binary-string manipulation (hashing and Salsa20 encryption primitives) will reduce the speed and/or increase the memory footprint of a JS implementation. This overhead may be bad enough to lose the advantage that scrypt offers.

A JS implementation is necessary for the use-cases in which BrowserID support is shimmed into a browser without native support. When native support is available, the scrypt code can be written in C++ and run at full speed. However, for BrowserID to achieve general deployment, the shimmed case is required, so some form of scrypt-without-native-C++ is needed.

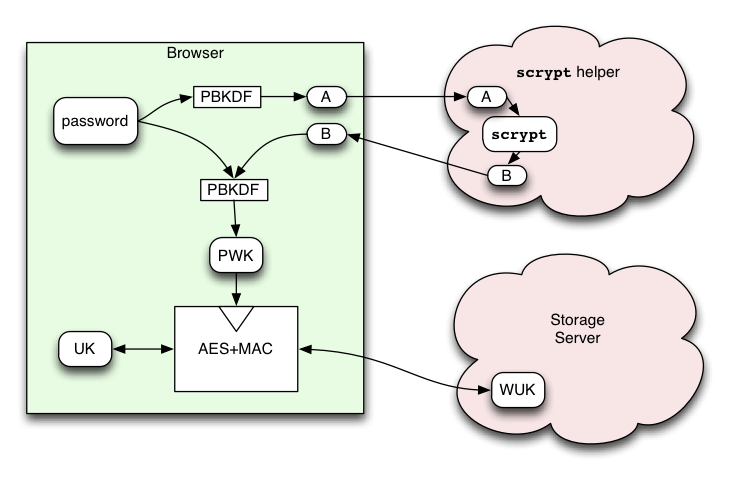
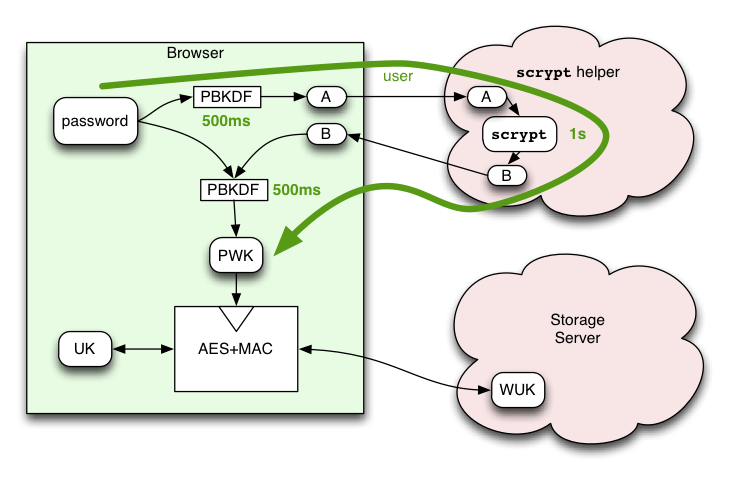
So here's a crazy idea: outsource the scrypt calculation to a semi-trusted server. The browser code first spends 500ms computing 23k iterations of PBKDF to generate an intermediate "A" value. It then sends A to the scrypt Helper, a service that we run (separate from the Storage Server). The Helper spends one second computing the scrypt function, then returns the derived "B" value. The Helper then carefully forgets everything about the computation.

The browser receives the B value, then spends another 500ms computing PBKDF on it (using both B and the original password as secrets). It uses the result as the Password-Wrapping-Key (in the non-scrypt-enabled design, PWK=A).

scrypt-helper Costs/Attacks

Note: http://keywrapping.appspot.com hosts an interactive cost/latency calculator application to evaluate the parameters described here.

The user cost is a two-second delay for the initial login. The browser can cache the derived PWK value for the lifetime of the profile, so subsequent uses do not need to contact the helper or spend the 1s doing PBKDF. In theory, this means that each browser+user combination only needs to spend this time exactly once. (this may permit a longer scrypt step, perhaps 10s instead of 1s, raising the cost of attack by 10x).

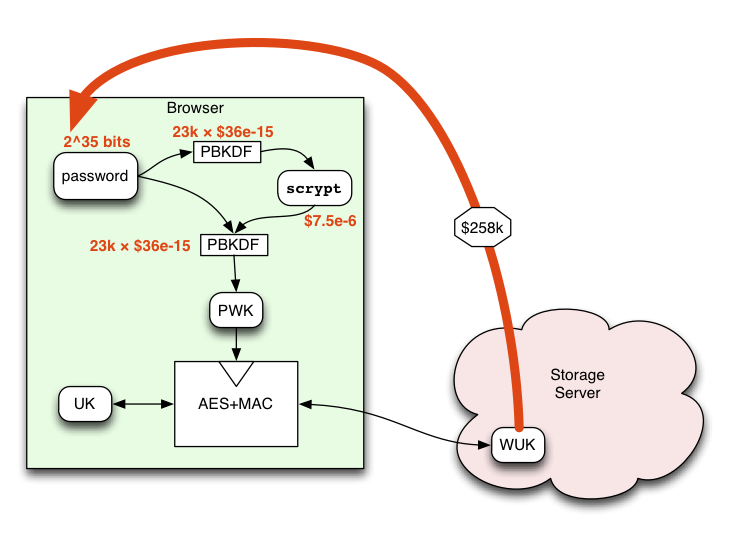
Adding scrypt() to the derivation chain raises the attack cost for the WUK-holding server (and friends) significantly. If we assume that the helper runs on an AWS EC2 m1.small instance (at today's spot cost of $0.027/hour), and that the attacker's hardware has similar costs, then they must spend about $7.5*10^-6 for each 1s guess (i.e. each dollar gets them 133k guesses). The PBKDF cost is negligible in comparison. This class of attacker must then spend about $258k to exhaust the 35-bit password space assumed above.

(note that an attacker with a one-million node botnet can perform the same amount of work in about 9.5 hours. I do not know what it costs to rent a 1M-node botnet for 10 hours.)

The Helper is, of course, a new category of attacker: it could misbehave and retain the "A" or "B" values, or an intruder might modify its code to do the same, or an eavesdropper might see "A" or "B" in transit. Knowledge of "A" allows an attack limited by the first PBKDF step. Knowledge of both "B" and the WUK allows an attack limited by the second PBKDF step. In both cases, the attack is no better than the one available to the Primary-Server-And-Friends in the only-PBKDF design.

The significant advantage, however, is that ex-post-facto attacks do not work. Once the Helper has correctly forgotten A and B, the window of vulnerability is closed. The hopeful attacker must compromise the Helper before the user begins their initial setup on a new browser, and must retain control until after the one-second window has closed. The Helper has zero long-term state and finishes each job in one second. This enables some useful security techniques, such as booting from read-only media and restarting the system at frequent intervals to "shake out" any intruders.

As with the PBKDF-only design, the Storage Server must remember the long-term WUK value to function correctly, however in this proposal the WUK does not provide the same low-cost attack vector.

(caveats: you should always be skeptical of models that claim to produce actual numbers. All the dollar costs here are intended as rough order-of-magnitude estimates, and various factors could result in excursions either way. For example, EC2 "t1.micro" instances might work just as well, and are 4x cheaper. Specialized hardware could compute scrypt() cheaper than an EC2 instance.)

local scrypt

For native implementations of the client-side protocol, the story is even better. These implementations can skip the Helper entirely, and perform scrypt in fast C++ code. The user cost is roughly the same (minus the latency of contacting the Helper).

However this completely removes the Helper-based attack, leaving only the $258k expensive WUK-based attack, available only to Server-and-Friends. In the long run, when all browsers have native implementations, this is a great position to occupy.

Write-Enabler Attacks, Details

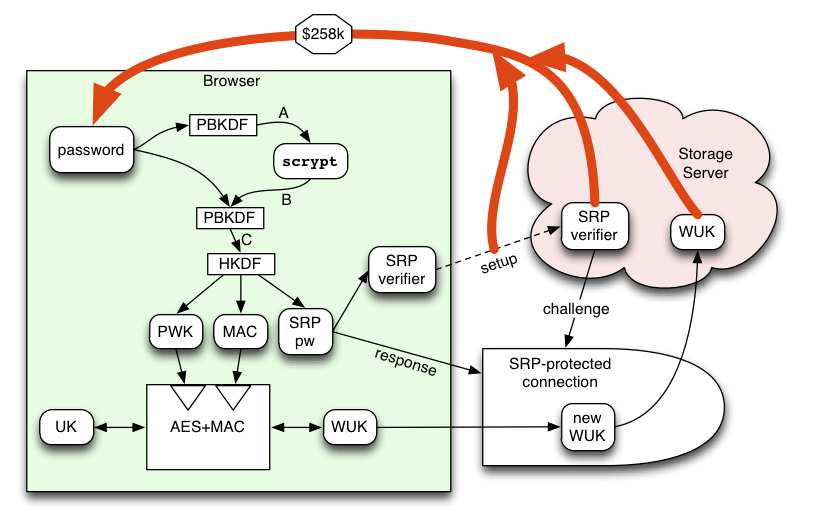
There are several details that need explanation, to avoid enabling cheaper attacks than the ones examined above. This diagram expands upon the previous design sketch. Note that the second PBKDF step actually generates three keys. The first is used to encrypt the User Key (UK). The second is used to MAC that data (necessary to protect the client against bit-flipping by the server, but which also serves as the oracle that enables the WUK-based attack). The third is used to prove the right to read or modify the server's stored WUK data, described below.

Fundamentally, the Storage Server holds a "mutable slot" that contains encrypted data. The client will frequently (perhaps once per browser session) fetch that encrypted data. Less frequently, that client will want to change the contents of the slot (once at account creation, later each time they change their password). The server will need to know when it is safe to permit either activity (so that attackers can't do them too). If it reveals the WUK to an attacker, they can (at some cost) try to get back to the password (or some equivalent). If it accepts a modification request from an attacker, the slot may be filled with invalid data, causing an availability/durability failure (the MAC won't match, so clients won't be tricked into accepting bad data, so it's not an integrity/confidentiality failure, but still pretty bad).

The "cold start" design requirement means that the password (or something derived from it) is the sole source of distinction between user and attacker. So the best we can do is to make sure that the "guess the read-enabler" and "guess the write-enabler" attacks are just as hard as the "guess the password" attack.

To avoid leaking the the WUK to a man-in-the-middle in the process of reading or updating it, we need a zero-knowledge protocol like SRP to establish a secure session between the client and the WUK-possessing server. SRP works by starting with a password and generating a "Verifier" from it. One side (the server) then holds the Verifier, while the client holds on to the password. Later, when the client wants to send a request, the server uses its Verifier to participate in a challenge-response protocol with the client. The result of this protocol is a session key that is 1: unknown to any eavesdropper, and 2: proof that the client knew the password from which the Verifier was derived. The session key is then used to encrypt and MAC the read or write request, along with the response. The ZKP properties of SRP mean that an eavesdropper really gets zero information about the password, no matter how many sessions they observe. As a result, using SRP to exercise the read-enabler or write-enabler does not give an MitM any advantage.

The Verifier, however, provides the same attack path as the WUK's MAC. Anyone who knows the Verifier could simply run the protocol against themselves as frequently as they liked. SRP adds a few large modular exponentiations, but these wouldn't increase the cost much beyond the scrypt step. The server knows the Verifier, but they also know the WUK, so get no additional advantage.

The remaining offline attack vector is the initial establishment of the SRP verifier. If an attacker is able to eavesdrop on the account-creation message, and learns the Verifier, they'll be able to mount the same attack as the server. To protect against this, the Verifier must either be sent in a good SSL connection for which the certificate has been tested against a known-correct value, or it needs to be encrypted before transit to a known-correct public key.

Online attackers who simply guess a password and then attempt to fetch the WUK (or modify it) can be rate-limited. By limiting guesses to once every 10 seconds per account, the persistent attacker would take about 10k years to exhaust a 35-bit keyspace. Attackers who MitM the client connection will not learn the SRP session key and won't be able to decrypt the message. On the other hand, a successful MitM on a shimmed browserid.org connection would simply serve broken JS that reveals the password instead of performing SRP. On the third hand, a native implementation would include the SRP code, and the browser-private data (like PWK) would not be available to web-sourced attack code regardless of origin, so the MitM attacker would be limited to the usual MitM attacks, which SRP protects against nicely.

The Helper communications must also be protected carefully. Clients must send their "A" value to a safe Helper, and both A and B must remain confidential in transit. Revealing these values would allow the eavesdropper to make the same cheap brute-force attack as the Helper. The same techniques described above (to establish the Verifier) must be applied here: checking an SSL certificate, or encrypting to/from a pre-established public key.

Server-Side Anonymous Data

It would be nice if the server's database were anonymous: while each row is definitely associated with a particular user (email address), if the server cannot figure out which is which, then many attackers won't either.

The benefit of this property would be that attackers who perform a brute-force search would be obligated to process more data, making their attack more expensive. Each row of the server's data includes a computationally-difficult function of an email address and a password. An attacker who is after a specific user's password knows the email address. If they also know which row holds that user's data, their task is to loop over all likely passwords, execute the function for each one, then compare the output value against that row.

An attacker who doesn't know which row is which must compare their output value against all rows. If you have the whole dataset, this is bulky but not computationally hard (O(logN)). The most likely attack against the scrypt step is a botnet, in which the controller would send each node the target email address and a subset of the password list. To detect success, either the controller must also send the whole dataset to each node, or the node can stream back the computed values to the controller for local membership checks, or something in between. The optimum attack probably has the controller distribute a Bloom Filter (9.6 bits per dataset row for a 1% false-positive rate, so about 120MB for a 100M-row table) and the nodes sending back potential matches for the controller to evaluate.

Both PBKDF steps require the target's email address, so if this is performed on the botnet node (and either the second PBKDF step must be run there, or the nodes must stream every intermediate "B" value back to the controller), then forensics may reveal which email address is being attacked. If detected, this may give the victim time to take action before the password is found.

The biggest benefit of anonymous data probably lies in the exfiltration step. Attackers who manage to run code on the storage server (i.e. a SQL injection), but who can't do some kind of traffic-analysis (correlating the target's login time with database access patterns), won't know which rows to extract. Extracting the important information from all rows (perhaps 6.4GB of data for a 100M-user table) would be a massive download, easily detectable and preventable by basic monitoring tools. This helps against a rogue-code attacker, but not against one who gets a full copy of a backup tape, or coerces the server operator into providing full access.

To accomplish server-side anonymous data, the KDF and Setup steps need to wind up with an identifier that points to a specific row of the database, but which is hard to correlate with an email address. Anyone (the user) who knows both the email address and password should be able to get this identifier (and, since this is a "cold start" protocol, it must be able to work with nothing but an email+password), which does limit our options somewhat.

Protecting the storage selection index

I think we can tolerate a "TOFU" (Trust On First Use) setup step, especially if it is protected by a pinned-SSL implementation (i.e. implemented in a browser that overcomes the limitations of the XHR API, where you might prefer to tell XHR what SSL certificate you expected to see, by using and enforcing an embedded table of name-to-CA or name-to-cert mappings). But it'd be nice to only rely on this once: TOFU, not TOE-U (Trust On Every Use). With TOFU it should be safe to run the later communications in plaintext (with SSL providing an extra layer of safety).

To accomplish this, nothing in the post-setup messages should give an attacker a way to brute-force the password (reserving that "power" for the storage server), including the field that tells the server which database row to use. This constraint precludes the use of anything that is derived from the password, leaving us with two choices:

• the non-secret email addres
• a random nonce generated by the server, retrieved in the TOFU step, remembered on the client

The first choice loses the "anonymous data" property on the server. The second choice loses the server's ability to do per-user rate-limiting of online guessing attacks (but retaining other tools, like per-IP-address limiting of non-distributed attacks). I'm still trying to decide which is more important, or if there is some clever way to achieve both.

Protocol Diagram

The following PDF diagrams contains complete details on several variants of the protocol, including how the salts are generated, and the client/server messages that are exchanged.

• anonymous data, no SRP
• anonymous data, yes SRP
• email-indexed data, yes SRP

In each document, the first page describes the basic KDF operation and the "init" message which establishes or retrieves the user's SRP verifier or (for the non-SRP case) their "S2" selection index and "S3" shared secret. The second page shows how SRP or S2+S3 are used to perform protected requests. The third page shows the "get" and "set" protected requests. The final page shows the "change password" request (which combines a "get" request, to fetch the UK, then uses a new "change" message to replace the stored data with a re-encrypted row). There is also a "delete data" request that is similar for all variants.

The anonymous-data forms never reveal the user's email address to the server, which somewhat increases an attacker's costs, but prevents account-based rate-limiting of online attacks. In all cases the "TOFU" window exists only during the init phase: once that setup has been performed, all subsequent messages could safely be sent in the clear.

Implementation-Driven Changes

NSS, the cryptographic library used in Firefox, is enthusiastic about keeping key material behind a notional barrier (retaining the ability to implement primitives on a smart card or HSM). So its KDF functions don't want to reveal the derived keys, since they're "keys" and not "data". To overcome this (and make it easier to take advantage of NSS, instead of reimplementing many primitives), the protocol needs to sneakily derive values from the "keys".

I'm still working through what changes are necessary to support this, but at first glance, we'll need to define an EXTRACT function that encrypts a block of zeros (equal in length to the key size), using the derived key as the encryption key, and use the resulting "ciphertext" as the output of the KDF step. For example, instead of A=PBKDF(args), we'd use A0=PBKDF(args) and A=AES(key=A0).encrypt(plaintext=000). That lets us get "A" outside the NSS barrier and either deliver it to the scrypt-server or into the next KDF step (probably passing it back *into* the barrier).

We'll need this EXTRACT step after the first round of PBKDF (on "A"), after the scrypt step on "B", and after the second round of PBKDF (on "C", giving us the option of storing "C" in the password manager). If HKDF is provided by NSS too, we'll have to do it again on each of the outputs of the HKDF step (PWK, MAC, and S1/SRPpw).

Updates / Discussion

• 10-Apr-2012: updated cost model: EC2 spot prices are 3x lower than on-demand, lowering scrypt "expensive" attack from $750k to $258k -warner
• note that the current plan is to *not* store the WUK on a Primary IdP, but only on a mozilla server -warner
• 17-Apr-2012: PBKDF2, when used to create 3 keys, takes 3 times as long (i.e. we get one third the protection for a given user delay). I'd rather generate multiple keys with the HKDF expansion step, which is safe but doesn't repeat the stretching. And once we're using that, it easier to write the spec if we use the HKDF extraction step too (even though it's unnecessary here: the output of PBKDF is already uniform). So I'm going to rewrite that part to use do C=PBKDF2(P=join(B,password),S=constant), PWK,MAC,SRPpw=HKDF(XTS=constant, SKM=C, CTXinfo="", L=3*256/8).
• I'm going to try cross-compiling the scrypt() code to JS with Emscriptem to see how much of a slowdown we get. On Chrome, we could use conceivably use NaCl to run the scrypt() code at full speed, although currently they're only allowing NaCl code to run inside apps downloaded from their app store.
• the scrypt parameters (and PBKDF ones too) must be the same for all devices accessing the same account. If they aren't baked into the client code, the first device must choose them (and hope they aren't too slow for the other devices), MAC them with a derived KEY, then store the parameters on the server along with the SRP salt. Later, clients must fetch and use the parameters to derive the keys, then check the MAC before revealing any information about the derived keys. The goal is to prevent a server from providing artificially low parameters in the hopes of learning a less-well-protected oracle. There is subtlety here that needs thought.
• 01-May-2012: following Ben's advice, I'm updating this to remove email addresses from the Storage Server, instead indexing its storage with anonymous "account IDs", derived in the HKDF step along with the wrapping key and the SRP password. The only wrinkle is that we need to use a fixed SRP salt.
• 01-Mar-2012: bitcoin miners are moving to FPGAs, dropping the likely cost of dedicated SHA256 hashing by perhaps 10x.
• 15-May-2012: Stefan Arentz did some PBKDF benchmarking on mobile devices: https://wiki.mozilla.org/SJCL_PBKDF2_Benchmark . Looks like it takes 3ms/round on the slowest device (iPod Touch 2G), and .14ms/round on a Galaxy Tab (compared to more like 20us/round on a laptop). So we need to decide what the slowest device we'll support well, and use however many rounds 500ms takes on that machine.